(Originally posted on Scientia Salon)
11. September 2014.
Ever since the formulation of Newton’s laws of motion (and maybe even before that), one of the popular philosophical ways of looking at the world was determinism as captured by the so-called "Clockwork Universe" metaphor. This has raised countless debates about various concepts in philosophy, regarding free will, fate, religion, responsibility, morality, and so on. However, with the advent of modern science, especially quantum mechanics, determinism fell out of favor as a scientifically valid point of view. This was nicely phrased in the famous urban legend of the Einstein-Bohr dialogue:
Despite all developments of modern science in the last century, a surprising number of laypeople (i.e., those who are not familiar with the inner workings of quantum mechanics) still appear to favor determinism over indeterminism. The point of this article is to address this issue, and argue (as the title suggests) that determinism is false. Almost.
Let us begin by making some more precise definitions. By "determinism" I will refer to the statement which can be loosely formulated as follows: given the state of the Universe at some moment, one can calculate a unique state of the Universe at any other moment (both into the future and into the past). This goes along the lines of Laplace’s demon and physical determinism, with some caveats about terminology that I will discuss below. Of course, there are various other definitions of the term "determinism" (see here for a review) which are not equivalent to the one above. However, the definition that will concern us here appears to be the only one which can be operationally discussed from the point of view of science (physics in particular) as a property that Nature may or may not possess, so I will not pursue any other definition in this article.
There are various caveats that should be noted regarding the definition of determinism. First and foremost, regarding the terms "Universe", "moment", "past" and "future", I will appeal to the reader’s intuitive understanding of the concepts of space, time and matter. While each of these can be defined more rigorously in mathematical physics (deploying concepts like isolated physical systems, foliated spacetime topologies, etc...), hopefully this will not be relevant for the main point of the article.
Second, I will deploy the concept of "calculating" in a very broad sense, in line with the Laplace’s demon --- assume that we have a computer which can evaluate algorithms arbitrarily fast, with unlimited memory, etc. In other words, I will assume that this computer can do whatever can "in principle" be algorithmically calculated using math, without any regard to practical restrictions on how to construct such a machine. I will again appeal to the reader’s intuition regarding what can be "calculated in principle" versus "calculated in practice", and I will not be limited by the latter.
Finally, and crucially, the concept of the "state" of a physical system needs to be formulated more precisely. To begin with, by "state" I do not consider the quantum-mechanical state vector (commonly known as the wavefunction), because I do not want to rely on the formalism of quantum mechanics. Instead, for the purposes of this article, "state" will mean any set of particular values of all independent observables that can be measured in a given physical system (a "phase space point" in technical terms). This includes (but is not limited to) positions, momenta, spins, etc. of all elementary particles in the Universe. In addition, it should include any potential additional observables which we are unaware of --- collectively called hidden variables, whatever they may be.
We all know that quantum mechanics is probabilistic, rather than deterministic. It describes physical systems using the wavefunction, which represents a probability amplitude for obtaining some result when measuring an observable. The evolution of the wavefunction has two parts --- unitary and nonunitary --- corresponding respectively to deterministic and nondeterministic. Therefore, if determinism is to be true in Nature, we have to assume that quantum mechanics is not a fundamental theory, but rather that there is some more fundamental deterministic theory which describes processes in nature, and that quantum mechanics is just a statistical approximation of that fundamental theory. Thus the concept of "state" described in the previous paragraph is defined in terms of that more fundamental theory, and the wavefunction can be extracted from it by averaging the state over the hidden variables. Consequently, in this setup the "state" is more general than the wavefunction. This is also illuminated by the fact that in principle one cannot simultaneously measure both the position and the momentum of a particle, while in the definition above I have not assumed any such restriction for our alleged fundamental deterministic theory.
As a final point of these preliminaries, note that the concept of the "state" can be defined rigorously for every deterministic theory in physics, despite the vagueness of the definition I gave above. The definition of state always stems from specific properties of equations of motion in a given theory, but I resorted to the handwaving approach in order to avoid the technical clutter necessary for the rigorous definition. In the remainder of this article, some math and physics talk will necessarily slip in here and there, but hopefully it will not interfere with the readability of the text.
Given any fundamental theory (deterministic or otherwise), one can always rewrite it as a set of equations for the state --- i.e., equations for the set of all independent observables that can be measured in the Universe. These equations are called effective equations of motion, and they are typically (although not necessarily) partial differential equations. This sets the stage for the introduction of our four main players:
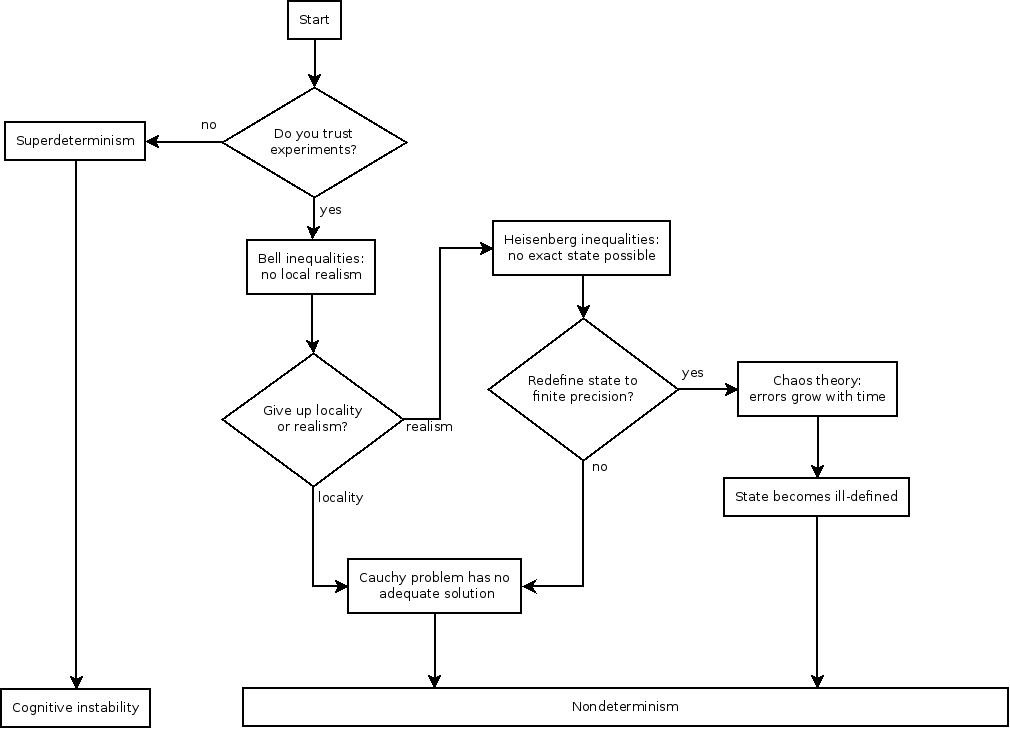
which will team up to provide a proof that the effective equations of motion of any deterministic theory cannot be compatible with experimental data.
Let us first examine the main consequence of the experimental violation of Bell inequalities. Simply put, the violation implies that local realism is false, i.e., that any theory which assumes both locality and realism is in contradiction with experiment. In order to better understand this as it regards our effective equations of motion, let me explain what locality and realism actually mean in this context. Locality is an assumption that the interaction between two pieces of a physical system can be nonzero only if the pieces are in close proximity to each other, i.e., both are within some finite region of spacetime. The region is most commonly considered to be infinitesimal, such that the effective equations of motion for our deterministic theory are local partial differential equations. Such equations depend on only one point in spacetime (and its infinitesimal neighborhood), as opposed to nonlocal partial differential equations, which depend on more than one spacetime point. The point of this is to convince you that locality is a very precise mathematical concept, and that it may or may not be a property of the effective equations of motion. Realism is an assumption that the state of a physical system (as I defined it above) actually exists in reality, with infinite precision. While we may not be able to measure the state with infinite precision (for whatever reasons), it does exist in the sense that the physical system always is in fact in some exact well-defined state. While such an assumption may appear obvious, trivial or natural at first glance, it will become crucial in what follows, because it might be not true, from the experimental point of view.
The next ingredient is the experimental validity of Heisenberg inequalities. These inequalities essentially state that there are observables in nature which cannot be measured with infinite precision for the same state. And this means not even in principle, despite any technological proficiency that one may have at one’s disposal. The most celebrated example of this is the uncertainty relation between the position and momentum of the particle. Measuring the position places a finite boundary on measuring the momentum, and vice versa. Given that every state contains the positions and momenta of all particles in the Universe, Heisenberg inequalities are prohibiting us from being able to experimentally specify (i.e., measure) a single state of our physical system.
The third ingredient is a lesson in math --- the Cauchy problem. Given a set of partial differential equations, they typically have infinitely many solutions. The Cauchy problem is the following question: how much additional data does one need to specify in order to uniquely single out one particular solution out of the infinite set of all solutions? This additional data are usually called "boundary" or "initial" conditions. The answer to the Cauchy problem, loosely formulated is the following: for local partial differential equations, it is enough to specify the state of the system at one moment in time as the initial data. In contrast --- and this is an important and often under appreciated detail --- for nonlocal equations of motion this does not hold: the amount of data needed to single out one particular solution is much larger than that needed to specify the state of the system at any given moment, and is usually so large that it is generically equivalent to specifying the solution itself. In other words, given some nonlocal equations, in order to find a single solution of the equations, one needs to specify the whole solution in advance.
The final ingredient is another lesson in math --- chaos theory. It is essentially a study of solutions of nonlinear partial differential equations (usually restricted to local equations, so that the Cauchy problem has a solution --- this is called "deterministic chaos"). Chaos theory asks the following question: if one chooses a slightly different state as initial data for the given system of equations, what will happen to the solution? The answer (again, loosely formulated) is the following: for linear equations the solution will be also only slightly different from the old one, while for nonlinear equations the solution will soon become very different from the old one. In other words, nonlinear equations of motion tend (over time) to amplify the error with which initial conditions are specified. This is colloquially known as the butterfly effect.
Now we are ready to put it all together, and demonstrate that a deterministic description of nature does not exist. Start by imagining that we have formulated some fundamental theory of nature, and have specified all possible observables that can be, well, observed. Then we ask the question "Can this theory be deterministic?" given the definition of determinism provided at the outset. As a first step in answering that question, we formulate the effective equations of motion. Analysis of the Cauchy problem of the effective equations (whatever they may look like) tells us the following. If the equations are nonlocal, specifying the state of the system at one moment is not enough to obtain a unique solution of the equations, i.e., one cannot predict the state of the system neither for future nor for past moments. This is a good moment to stress the word "unique" in the definition of determinism --- if the initial state of the system produces multiple possible solutions for the past and the future, it is pretty meaningless to say that the future is "determined" by the present. So, in order to save determinism, we are forced to assume locality of the effective equations of motion.
Enter Bell inequalities --- we cannot have both locality and realism. And since we need locality to preserve determinism, we are forced to give up realism. But denial of realism means that the state describing the present moment (our initial data) does not exist with infinite precision! As I discussed above, this actually means that Nature does not exist in any one particular state. The best one can do in such a situation is to try to measure the initial state as precisely as (theoretically) possible, thereby specifying the initial state with at least some finite precision.
Enter Heisenberg inequalities --- there is a boundary on the precision with which we can measure the initial state of the system, and in absence of realism, there is a boundary on the precision with which the initial state can be said to actually exist. But okay, one could say, so what? Every physicist knows that one always needs to keep track of error bars, what is the problem? It is that the solution of the Cauchy problem assumes that the initial condition is provided with infinite precision. If the initial condition does not exist with infinite precision, the best one can do is to provide a family of solutions for the equations of motion, as opposed to a single, unique solution. This defeats determinism.
But wait, we can calculate the whole family of solutions, and just keep track of the error bars. If they remain reasonably small in the future and in the past (and by "reasonably small" we can mean "of the same order of magnitude as the errors in the initial data"), we can simply claim that this whole family of solutions represents one deterministic solution. Just like the initial state existed with only finite precision, so do all other states in the past and the future. Why cannot this be called "deterministic"?
Enter chaos theory --- if the effective equations of motion are anything but linear (and they actually must be nonlinear, since we can observe interactions among particles in experiments), the error bars from the initial state will grow exponentially as time progresses. After enough time, the errors will grow so large that they will always encompass multiple very different futures of the system. Such a situation cannot be called "a single state" by any useful definition. If we wait long enough, everything will eventually happen. This is not determinism in any possible (even generalized) sense, but rather lack thereof.
So it turns out that we are out of options --- if the effective equations of motion are nonlocal, determinism is killed by the absence of a solution to the Cauchy problem. If the equations are local, the initial condition cannot exist due to lack of realism. If we try to redefine the state of the system to include error bars, the Heisenberg inequalities will place a theoretical boundary on those error bars, and chaos theory guarantees that they will grow out of control for future and past states, defeating the redefined concept of "state", and therefore determinism.
And this concludes the outline of the argument: we must accept that the laws of Nature are intrinsically nondeterministic.
At this point, two remarks are in order. The first is about the apparently deterministic behavior of everyday stuff around us, experience which led us to the idea of determinism in the first place. After all, part of the point of physics, starting from Newton, was to be able to predict the future, one way or another. So if Nature is not deterministic, how come that our deterministic theories (like Newton’s laws of motion, or any generalization thereof) actually work so well in practice? If there is no determinism, how come we do not see complete chaos all around us? The answer is rather simple --- in some cases chaos theory takes a long time to kick in. More precisely, if we consider a small enough physical system, which interacts with its surroundings weakly enough, and it is located in a small enough region of space, and we are trying to predict its behavior for a short enough future, and our measurements of the state of the system are crude enough to begin with --- we might just get lucky, so that the the error bars of our system’s state do not increase drastically before we stop looking. In other words, the apparent determinism of everyday world is an approximation, a mirage, an illusion that can last for a while, before the effects of chaos theory become too big to ignore. There is a parameter in chaos theory that quantifies how much time can pass before the errors of the initial state become substantially large --- it is called the Lyapunov time. The pertinent Wikipedia article has a nice table of various Lyapunov times for various physical systems, which should further illuminate the reason why we consider some of our everyday physics as "deterministic".
The second remark is about the concept of superdeterminism. This is a logically consistent method to defeat the experimental violation of Bell inequalities, which was crucial for our argumentation above. Simply put, superdeterminism states that if the Universe is deterministic, we have no reason to trust the results of experiments. Namely, an assumption of a deterministic Universe implies that our own behavior is predetermined as well, and that we can only perform those experiments which we were predetermined to perform, specified by the initial conditions of the Universe (say, at the time of Big Bang or some such). These predetermined experiments cannot explore the whole parameter space, but only predetermined set of parameters, and thus may present biased outcomes. Moreover, one has trouble even defining the concepts of "experiment" and "outcome" in a superdeterministic setup, because of the lack of experimenter’s ability to make choices about the experimental setup itself. In other words, superdeterminism basically says that Nature is allowed to lie to us when we do experiments.
In order to understand this more clearly, I usually like to think about the following example. Consider an ant walking around a 2-dimensional piece of paper. The ant is free to move all over the paper, it can go straight or turn left and right. There are no laws of physics preventing the ant from doing so. A natural conclusion is to deduce that the ant lives in a 2-dimensional world. But --- if we assume a superdeterministic scenario --- we can conceive of initial conditions for the ant which are such that it never ever thinks (or wishes, or gets any impulse or urge, or whatever) to go anywhere but forward. Such an ant would (falsely) conclude that it lives in a 1-dimensional world, simply because it is predetermined to never look sideways. So the ant’s experience of the world is crucially incomplete, and leads it to formulate wrong laws of physics to account for the world it lives in. This is exactly the way superdeterminism defeats the violation of Bell inequalities --- the experimenter is predetermined to perform the experiment and to gather data from it, but he is also predetermined to bias the data while gathering it, and to (falsely) conclude that the inequalities are violated. Another experimenter on the other side of the globe is also predetermined to bias the data, in exactly the same way as the first one, and to reach the identical false conclusion. And so are a third, fourth, etc. experimenters. All of them are predetermined to bias their data in the same way because the initial conditions at the Big Bang, 14 billion years ago, were such as to make them do so.
This kind of explanation, while logically allowed, is anything but reasonable, and rightly deserves the name of superconspiracy theory of the Universe. It is also a prime example of what is nowadays called cognitive instability (I first encountered the term “cognitive instability” as used by Sean Carroll, though I am not sure if he coined it originally). If we are predetermined to skew the results of our own experiments of Bell inequalities, it is reasonable to expect that other experimental results could also be skewed. This would force us to renounce experimentally obtained knowledge altogether, and to the question why to even bother to try to learn anything about Nature at all. Anton Zeilinger has phrased the same issue as follows:
"[W]e always implicitly assume the freedom of the experimentalist ... This fundamental assumption is essential to doing science. If this were not true, then, I suggest, it would make no sense at all to ask nature questions in an experiment, since then nature could determine what our questions are, and that could guide our questions such that we arrive at a false picture of nature."
Let me summarize. The analysis presented in the article suggests that we have only two choices: (1) accept that Nature is not deterministic, or (2) accept superdeterminism and renounce all knowledge of physics. To each his own, but apparently I happen to be predetermined to choose nondeterminism.
It is a fantastic achievement of human knowledge when it becomes apparent that a set of experiments can conclusively resolve an ontological question. And moreover that the resolution turns out to be in sharp contrast to the intuition of most people. Outside of superconspiracy theories and "brain in a vat"-like scenarios (which can be dismissed as cognitively unstable), experimental results tell us that the world around us is not deterministic. Such a conclusion, in addition to being fascinating in itself, has a multitude of consequences. For one, it answers the question "Is the whole Universe just one big computer?" with a definite "no". Also, it opens the door for the compatibility between the laws of physics on one side, and a whole plethora of concepts like free will, strong emergence, qualia, even religion --- on the other. But these are all topics for some other articles.
At the end, here is a helpful flowchart, which summarizes the main lines of arguments of the article:
_____
Marko Vojinovic is a theoretical physicist, doing research in quantum gravity at the University of Lisbon. His other areas of interest include the foundational questions of physics, mathematical logic, philosophy, knowledge in general, and the origins of language and intuition.